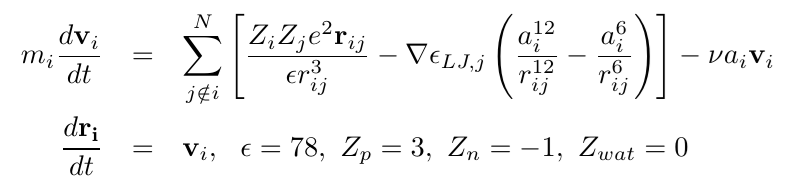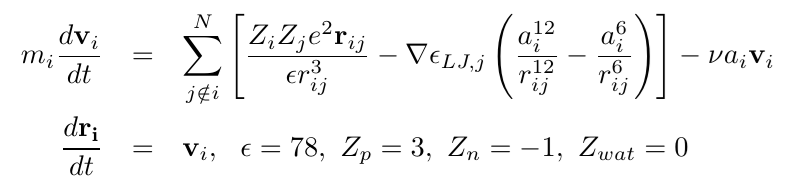
高分子の生体現象では，大きな電荷反転の現象 (電荷の中性条件
を大きく越えた電荷) が起きている。これを応用すると，微小DNAの
人体内の輸送が可能である (Refs. 1-5)。これが起きるためには
2つの条件が必要であり，
1) マクロイオンから見て，2価以上の対イオンがあること，
2) クーロン相互作用が熱的レベルを越えて起きること，
である。Langevinの熱浴効果がクーロン力，LJ力に加わるため，
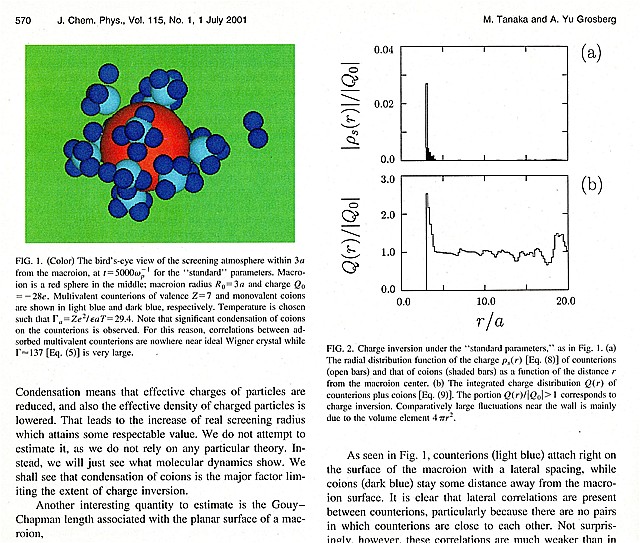
マクロイオン(負電荷) の表面近くに正電荷のイオンが集まっている。
反発力で振動する正と負の電荷とは違って，生体では熱浴による
温度調節(thermostat) が効いて，普通に振動は減衰していく。

ここでは，マクロイオン，正負のイオン、中性の水分子を扱って
いて，正方形の周期的境界条件を与えている。マクロイオンは，
Q_mac=-30e, R_mac=5a, M=300mで，正電荷イオンは110個，
負電荷イオンは300個，正方格子の約67 オングストローム，
水分子は約3.2 オングストロームごとに置き 8000個である。
(CGS系：e=4.80x10^-10 esu, m=1.67x10^-24 g, a=1.0x10^-8 cm,
..t=1.0x10^-15 s (1 fs), \eps=78, Zcn=3, Zcn=-1, Zwat=0)

大切なことは，クーロン力を実空間の近距離力とフーリエ空間
の遠距離力に分けて計算する。２つの相互作用を分離して，
良い精度でクーロン力を計算できる (Ref. 6, Deserno and Holm,
1998, Ref.7, https://github.com/Mtanaka77/Charge_inversion)

クーロン力を分離しないときは，非周期系のプラズマ発展問題
や生体現象などで，電場 \E = -\nabla(Z_{i}Z_{j} e_unit^2/r) を
用いる。C+Auなどの爆発現象 (Ref.8)や，分子スケールのナノ孔
DNA輸送である (Ref. 5)。そこでは分子動力学法と電場を実空間
だけで扱っている。
　それと異なり，セル内粒子（Particle-in-Cell）の短い「ディバイ長」
の平均近似で，空間メッシュで電場を解く場合であり，応用は
プラズマの平均値問題や核融合分野などに限られる。

価数が2価原子ではCa, Fe, Zn，3価原子ではAl, Feなど，分子
イオンではDNAの一部であるPO_4^- がある。錯イオンでは, 1価の
[Al(OH)_4]^1-, 2価の[Zn(NH3)^4]^2+, 3価の[Fe(CN)_6]^3-, 4価の
[Zn(OH)_4]^4-, [Fe(CH)_6]^4-, などがある。

* FortranとMPI による並列計算
高性能の6-12 Core以上をもつパソコンでは，Fortranを使い並列
計算MPI で効率的に分子動力学シミュレーションを計算している。
計算速度からLinux 64-bit PCが使われるが，Windowsパソコンで
VirtualBoxを計算窓に置くことで，Linux窓にログインして使える。
Linuxコマンドを勉強することが必須であるが，Linuxコマンドは
単純であり習得しやすい。

高速計算のために，C言語ではなくFortran言語を使い，MPICH，
FFTW3のパッケージが必要である（Linuxのネットワーク上で無料で
ダウンロードできるので，費用はかからない）。
　複数コアで並列演算するための MPI手法では，並列処理でコアに
割り振るため，等間隔飛ばしdoループや多重ループ処理が普通に
使われる (連続切り出しdoループは効率が悪い！)

並列演算とベクトル演算の効率に関しては2019年夏のデータがある。
分子動力学シミュレーションにおいて測定すると，並列計算（富士通,
FX100）と並列/ベクトル計算(NEC, Aurora）において，演算速度は後者を
基準とすると前者は約3倍の速度である。

Go to the homepage