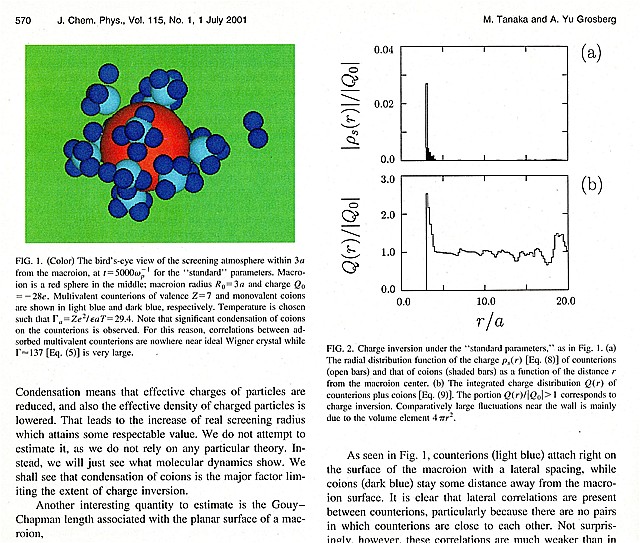
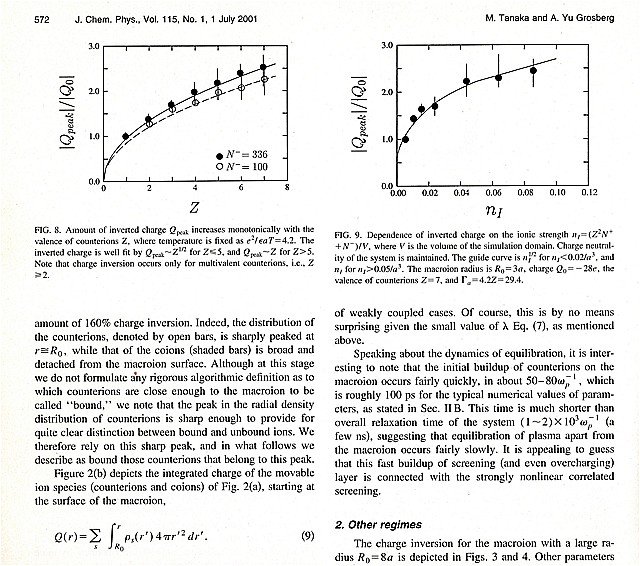
Two conditions for charge inversion of the electrolyte:
1. Counterions must be multivalently charged, Z= 2, 3 or more,
2. Coulomb interactions must be strong compared to thermal energy.
Macroion charge Q= -30e, its radius R=5a and M=300m, and
Zcp=3, Zcn=1, \epsilon=78 at 27 deg Celsius. For Z=2, Ca, Fe, Zn;
for Z=3, Al, Fe; for complex ions, [PO_4]^4- in DNA, ...
(CGS unit system: e=4.8x10^-10 esu, m=1.66x10^-24 g, a=1x10^-8 cm,
\epsilon=78, epsilon_LJ is given in Ref.1)

By Langevin thermostat of the third term on top of Coulomb forces, the
macroion is rather stationary due to water molecules, and absorbs many
counterions at r= Rmac and Rmac+10a. The figure of the macroion and
counterions shows the occurrence of charge inversion in Ref. 1 and Ref.
2-5.
References
1. M. Tanaka and A.Yu Grosberg, J.Chem.Phys., vol.115, 567-574 (2001).
2. M. Tanaka and A.Yu Grosberg, Euro.Phys.J., E7, 371-379 (2002).
3. M. Tanaka, Phys.Reviews., E68, 061501 (2003).
4. M. Tanaka, J. Physics: Condensed Matter, vol.16, S2127-2134 (2004).
5. Y.Rabin and M.Tanaka, Phys.Rev.Lett., vol.94, 148103 (2005).
Go to the homepage
,
M. Tanaka and A. Grosberg, J.Chem.Phys., 115, 567 (2001).
We report molecular dynamics simulation of the (overall neutral) system
consisting of
an immobile macroion surrounded by the electrolyte of multivalent counterions
and
monovalent coions. In a short time (< a few nanoseconds), counterions adsorb on the
macroion surface in the amount much exceeding neutralization requirement,
thus
effectively inverting the sign of the macroion charge. We find two conditions
necessary
for charge inversion, namely, counterions must be multivalently charged and Coulomb
interactions must be strong enough compared to thermal energy. On the other hand,
coion condensation on the multivalent counterions similar to Bjerrum pairing
is the
major factor restricting the amount of charge inversion. Depending on parameters,
we observe inverted charge up to about 200% the original charge of the macroion in
absolute value. The inverted charge scales as ζ^(1/2) when ζ<1 and crosses over to
ζ for ζ>1, where ζ= (A_0/r_s)^2, r_s is the Debye screening length in the electrolyte
and A_0 is the distance between adsorbed counterions under neutralizing conditions.
These findings are consistent with the theory of “giant charge inversion”
[Phys. Rev. Lett.
85, 1568 (2000)].